
Recipe
Start with the set of “winged” tiles shown below. The content of a tile is shown within the dotted lines. “Wings” extend beyond the content area. (The gray background is not part of the tile, but is included so you can see the boundary of the white parts.) Successive tiles in the set are scaled by 1/2, and black and white are swapped at each step. The boundaries between black and white meet the dotted lines at 1/3 and 2/3:
 …
…
Assemble tiles by adjoining along the dotted lines, letting the wings overlap adjacent tiles. Place smaller tiles on top of larger tiles:

Tiles can be assembled in lots arrangements, for example, random, regular, or filling arbitrary areas:

When you replace the squares with tile motifs, you get interesting patterns:

By joining the connection points on the edges of tiles in various ways, you get various motifs:
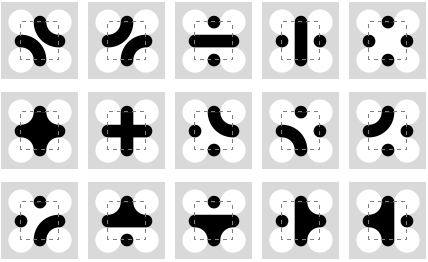
Mixing those motifs gives more variety of pattern, and interesting emergent forms:

Gallery
History
“Truchet tiles” originate with a treatise by Sebastien Truchet published in 1704, Mémoir sur les Combinaisons, in which Truchet investigates the kinds of patterns that can be made with a simple square tile divided diagonally, white on one side and black on the other. Cyril Stanley Smith popularized the idea in his 1987 paper, The tiling patterns of Sebastian Truchet and the topology of structural hierarchy. Toward the end of that paper, Smith introduces a tile that has become the most popular representative of the idea of Truchet tiles:

When that tile is used in random orientations to produce a tiling, the curves join to form connected domains that can be colored alternately white and black, producing an infinity of patterns:

I wondered whether that concept could be made to work at multiple scales. If you replace Smith’s two arcs with four arcs that connect with the sides at 1/3 and 2/3, two points in a larger tile connect with points in adjoining smaller tiles:
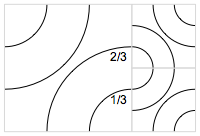
That leaves loose ends along an edge, but in any assembly of tiles you can always connect up the loose ends to form connected domains, as with Smith’s tiles. The winged tile trick gives you the colored domains automatically:

Sourcery
I developed the Wolfram Language package MultiScaleTruchetPatterns.wl to explore these patterns. Download this zip archive, uncompress, open the notebook MultiScaleTruchetPatternExamples.nb in Mathematica or Wolfram Desktop, and evaluate the expressions therein. The package is loaded on the first evaluation (answer “yes” when asked if you want to evaluate the initialization), which may take a while:
Linkery
Bridges 2018 paper: Multi-Scale Truchet Patterns
Lovely.
LikeLiked by 2 people
This is a really beautiful concept and has absolutely made my day! Trying it out myself now. Thank you 🙂
LikeLiked by 1 person
https://github.com/anetz89/truchetpattern
LikeLiked by 1 person
Check out the Twitter bots @Truchet_Nested and @Trichet_Nested from @SerinDelaunay which tweet randomly generated examples!
LikeLiked by 1 person
Thank you for this beautiful and detailed explanation
LikeLiked by 1 person
based on your work, with accreditation: https://www.instagram.com/p/CdEgeN_vN-I/
LikeLiked by 1 person
I love your work! Never seen anything like them before. For me, they are like Modernist Mandalas.
LikeLiked by 1 person
I love this idea – inspired by some of the bots generating them on social media, I made an interactive version at https://swift.swifteagle.co.uk/truchet
LikeLike
NiceI I like it.
LikeLike
This Truchet Multi-Scale pattern composer https://benergy80.github.io/TruchetMultiScale/ was built on the shoulders of your work here, and seeks to offer users some manual controls over composition creation.
LikeLike
Nice interface. Simple and effective. What platform was it developed with?
Had a look at ChiLab. Nice work.
LikeLike